前へ
実験一覧に戻る
ホームに戻る
[実験] ヒイラギモクセイの葉の棘の数の変異
3. 統計的検定とレポート作成
●母集団とサンプル
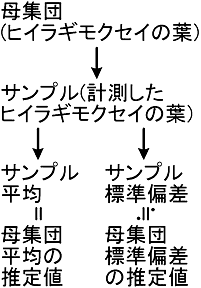 この実験では、数十枚の葉を計測することによって、ヒイラギモクセイの葉の性質について何らかの結果を出そうとしている。
この実験では、数十枚の葉を計測することによって、ヒイラギモクセイの葉の性質について何らかの結果を出そうとしている。
このようなとき、計測した葉のことをサンプル(または標本)と呼び、計測した葉もしなかった葉も含めて、全てのヒイラギモクセイの葉を母集団と呼ぶ。このように、サンプルの性質を調査することで母集団の性質を推定することを「標本調査」と呼ぶ。
この実験では、各グループごとに十分な数の葉を計測するようにした。また、計測するときに、偏った選び方をしないようにした。これは、この実験での調査対象が「計測したヒイラギモクセイの葉」ではなく「ヒイラギモクセイの葉」だからだ。つまり、例えば、平均や標準偏差を求めるのも、単に計測値の平均や標準偏差を求めるためだけではなく、母集団の平均や標準偏差を推定するためだ。
-
サンプルの平均は、母集団の平均の推定値である。推定の誤差は、サンプルのばらつきと正に相関し、サンプル数と負に相関する。言い換えると、数が多くて均一なサンプルで推定した母集団の平均は信頼性が高い。
-
サンプルの標準偏差は、ほぼ母集団の標準偏差の推定値と等しい(サンプルの標準偏差に[(サンプル数)/(サンプル数-1)]の平方根を掛けると母集団の標準偏差の推定値になる)。Excelの「STDEV」関数で求められる値は母集団の標準偏差の推定値の方になっている。
要するに、計測値に基づく平均や標準偏差(サンプルの平均や標準偏差)は一定の誤差を含む推定値だ。サンプルの平均に違いがあっても、母集団の平均に差がないと考えることはできない。どうしてかというと、母集団が同じでもサンプルにはよほどの偶然がない限り、多少の差が生じるからである。
サンプルの平均の間に差があっても、母集団の平均の間に差があるということにはならない。同じサイコロを同じように同じ回数(例えば10回)振っても、目の平均がぴったりと一致する方がむしろ珍しい。実力が全く同じチームどうしが試合をしても、大抵はどちらかが勝つ。打率が同じ2人のバッターであっても、ある1週間だけを取ってみると、大抵はどちらかが打率で勝っている。
それでは、母集団の平均の大小を論じることができないか、といえば、そうではない。サイコロ10回振りを何回も何回も繰り返して、それでも目の平均がかなり大きく違うとすると、サイコロそのものに違いがあると推定したくなる。多数の試合を繰り返して勝率にある程度の差があれば、チームの実力に差があると言ってもよいだろう。このような推定を論理的に行なうことは、統計的検定の役目の1つだ。
●統計的検定: 大小関係のt検定
大小関係の仮説は、平均値を比較することによって行なう。しかし、上で述べた理由で、単純に「計測値の平均値の大小」を結論とするわけには行かない。
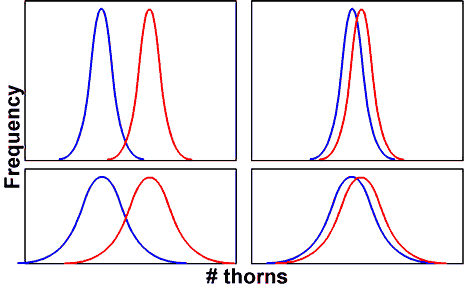 サンプルの平均値の差が大きいほど、母集団の平均に差がある可能性は高くなる(図の左と右)。また、サンプルの平均値の差が同じでも、サンプルのばらつきが大きければ、母集団の平均に差がある可能性は低くなる(図の上と下)。つまり、母集団の平均を比べようと思ったら母集団のばらつきも考慮する必要がある。また、平均や標準偏差は推定値だから、サンプル数も計算に入ってくる。
サンプルの平均値の差が大きいほど、母集団の平均に差がある可能性は高くなる(図の左と右)。また、サンプルの平均値の差が同じでも、サンプルのばらつきが大きければ、母集団の平均に差がある可能性は低くなる(図の上と下)。つまり、母集団の平均を比べようと思ったら母集団のばらつきも考慮する必要がある。また、平均や標準偏差は推定値だから、サンプル数も計算に入ってくる。
このように、サンプルのデータから母集団についての仮説に答えを与えることを「統計的検定」という。統計的検定の筋道は、数学の「背理法」に似ている。「棘の数の平均値のグループ間での差」の場合は、次のようになる。
この実験では、ExcelのTTEST関数を使い、「t検定」と呼ばれる統計的検定で、仮説を検証する。下では、統計的検定のあらすじを、t検定を例にとって説明する。
1. 統計量の計算
「統計量」とは、仮説の確かさを反映するようなパラメータで、ここでは、「スチューデントのt」と呼ばれる統計量を使う。統計量にはさまざまなものがあり、目的と条件によって適したものを選択する。今回の例では、本当は、tよりも適した統計量があるのだが、計算が楽なことを重視してあえてtで済ますことにする。
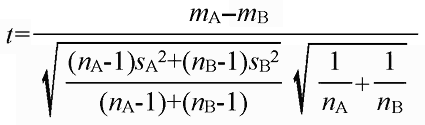
mA: グループAのサンプル平均
mB: グループBのサンプル平均
sA: グループAの標準偏差(母集団標準偏差の推定値)
sB: グループBの標準偏差(母集団標準偏差の推定値)
nA: グループAのサンプル数
nB: グループBのサンプル数
|
同じように葉の棘の数の高さによる違いを用い、より適切な検定(Kolmogorov-Smirnov検定)の例は、石居進「生物統計学入門」(培風館)のp.119 例16にある。ただし、初版では文章で「上の枝」と「下の枝」が逆になっている。先端葉と基部葉の違いでは、符号検定または符号順位検定が適している。
仮に nA = nB =n とすれば、
t2 = n × (mA ― mB)2/(sA2 + sB2)
になるから、サンプル平均の差が大きいほど、また、サンプル標準偏差が小さいほど、tは大きくなる。このことは、「平均の差が大きく、グループ内でのばらつきが小さいほど、仮説が正しい確率が高い」という感覚と合っている。
 2. 統計量の帰無分布の算出
2. 統計量の帰無分布の算出
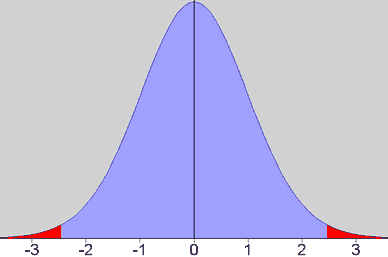
仮説の否定する仮説(サンプル平均の間に差はない)を仮定して、統計量tの確率分布をシミュレーションで求める。仮説を否定する仮説を「帰無仮説」といい、帰無仮説を仮定したときの統計量の確率分布を「帰無分布」という。サンプル平均の間に差がなければtは当然「いつでも0」かというと、そうはならず、0を中心とした釣り鐘型の分布(t分布: 右図)になる。
3. 帰無分布とデータから得られた統計量とを比較し、確率を求める
t分布にtと-tを当てはめ、それより外側に来る面積を求める。この面を「帰無仮説の元での確率」といい、tが0から離れるほど低くなる。上のグラフに、t=2.5の場合を当てはめると、紅く塗られた部分の全体に占める割合は約2%となる。
「帰無仮説の元での確率が約2%」ということの意味は、「帰無仮説の元で、このような高いtが出てくる確率が2%」ということだ。これは、イカサマのないサイコロで同じ目が3回出てくる確率(約2.7%)より低い。
今回の課題では、帰無仮説の元での確率が5%以下のときには、サンプルにおける違いは「母集団には差がないのに偶然出て来た差」ではない可能性が高い、つまり、母集団にも違いがある可能性が高い、と見なすことにする。このことを、統計を使ったレポートや論文では、「5%水準で統計的に有意な差がある」と表わす。「t = ××, P < 0.05」と略記することが多い。
TTEST関数によるt検定
Excelを使ってt検定をする場合は、上の1〜3の作業を自動化して、直接tとPの値を求めることができる。しかし、1〜3の筋道を理解して「帰無仮説の元での確率」の意味を理解しないと考察ができない。
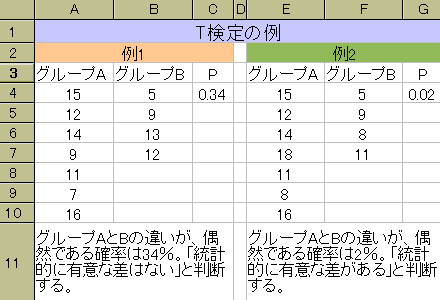
右の図は、2つのグループ(AとB)の差のt検定の例である。図だけで理解できない人は、同じファイルがここを右クリック→保存でダウンロードできるので、ダウンロードしたファイルを開いて確認できる。また、
hiiragiM-example1.xls
にもt検定の例が含まれている。
計測値の配置は、これと違っていても構わない。[C3]と[G3]のセルに、検定の結果(帰無仮説の元での確率)が計算されている。
t検定の結果を計算する式は、先端葉と基部葉の比較では、
=TTEST(グループAの値がある範囲,グループBの値がある範囲,2,1または3)
高さの違いによる比較では、
=TTEST(グループAの値がある範囲,グループBの値がある範囲,2,3)
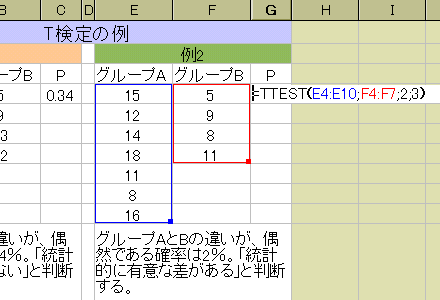 となる。[C3][G3]をダブルクリックすると右の図([G3]をダブルクリックした場合)のようになり、確認できる(確認したら、Escを押す)。最後の「,2,1」「,2,3」は、t検定にはいくつかの設定があるので、この実験に適した設定を指定している部分だ。
となる。[C3][G3]をダブルクリックすると右の図([G3]をダブルクリックした場合)のようになり、確認できる(確認したら、Escを押す)。最後の「,2,1」「,2,3」は、t検定にはいくつかの設定があるので、この実験に適した設定を指定している部分だ。
最初の数字は、1: 片側検定(決まった群について他方より大きいかそうでないかを調べる検定)、2: 両側検定(2群の間に差があるかを調べる検定)を示す。
後の方の数字は、1: 各データ間に対応関係がある場合、2: 対応関係が無く、2群の標準偏差が等しいと考えられる場合、3: 対応関係が無く、2群の標準偏差が等しいとは限らない場合、を示す。同じ枝の先端葉と基部葉のデータを対にしてデータを取っていた場合は「1」、そうでなければ「3」となる。高さの違いは、「3」でよい。
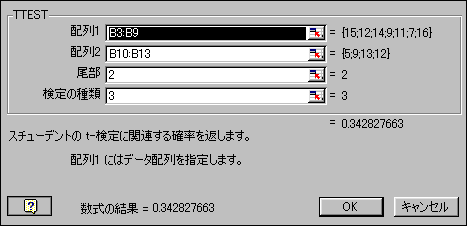 関数入力ウィンドウ(使い方の解説はここ)を使って入力するときは、図のようになる。
関数入力ウィンドウ(使い方の解説はここ)を使って入力するときは、図のようになる。
●棘の数と食害度
本来ならば統計的検定(順位相関係数による検定など)によって判断すべきだが、時間の都合で省略し、上の方で描いたグラフによって関係の有無を判断する。
以上の検定や判断を元に、「序論―材料と方法―結果―考察―参考文献」の構成を持ったレポートを作成してください。序論は、配付資料のものを、そのまま使うこと。レポート作成上で分からない点があったら、レポートの書き方を参考にしてください。提出期限は7月中旬(正確な日付は、後日知らせます)です。
前へ
実験一覧に戻る
ホームに戻る
 この実験では、数十枚の葉を計測することによって、ヒイラギモクセイの葉の性質について何らかの結果を出そうとしている。
この実験では、数十枚の葉を計測することによって、ヒイラギモクセイの葉の性質について何らかの結果を出そうとしている。 サンプルの平均値の差が大きいほど、母集団の平均に差がある可能性は高くなる(図の左と右)。また、サンプルの平均値の差が同じでも、サンプルのばらつきが大きければ、母集団の平均に差がある可能性は低くなる(図の上と下)。つまり、母集団の平均を比べようと思ったら母集団のばらつきも考慮する必要がある。また、平均や標準偏差は推定値だから、サンプル数も計算に入ってくる。
サンプルの平均値の差が大きいほど、母集団の平均に差がある可能性は高くなる(図の左と右)。また、サンプルの平均値の差が同じでも、サンプルのばらつきが大きければ、母集団の平均に差がある可能性は低くなる(図の上と下)。つまり、母集団の平均を比べようと思ったら母集団のばらつきも考慮する必要がある。また、平均や標準偏差は推定値だから、サンプル数も計算に入ってくる。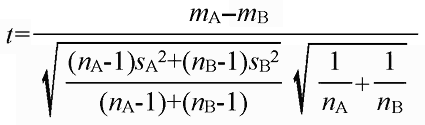
 2. 統計量の帰無分布の算出
2. 統計量の帰無分布の算出
 となる。[C3][G3]をダブルクリックすると右の図([G3]をダブルクリックした場合)のようになり、確認できる(確認したら、Escを押す)。最後の「,2,1」「,2,3」は、t検定にはいくつかの設定があるので、この実験に適した設定を指定している部分だ。
となる。[C3][G3]をダブルクリックすると右の図([G3]をダブルクリックした場合)のようになり、確認できる(確認したら、Escを押す)。最後の「,2,1」「,2,3」は、t検定にはいくつかの設定があるので、この実験に適した設定を指定している部分だ。 関数入力ウィンドウ(使い方の解説はここ)を使って入力するときは、図のようになる。
関数入力ウィンドウ(使い方の解説はここ)を使って入力するときは、図のようになる。